Les Arbres Binomiaux
On considère une séquence finie d’expériences dont chacune d’entre elles a un nombre fini de résultats possibles.
On se met donc dans notre cadre des marchés financiers qui peuvent soit monter soit baisser au cours de la journée et en prenant un espace temps considéré par notre style de Trading, qu’est le Scalping donc horizon court de 1 minute.
Les probabilités associées aux résultats possibles d’une expérience dépendent du résultat de l’expérience précédente ; il s’agit de probabilités conditionnelles. Pour représenter cette séquence, on utilise une représentation « en arbre », le théorème précédent permettant de calculer la probabilité de chaque feuille de l’arbre.
èLa probabilité qu’un chemin particulier de l’arbre se réalise est, d’après le théorème de la multiplication, le produit des probabilités de chaque branche du chemin.
1. Représentation des probabilités a priori et a postériori sur un arbre binomial à 2 temps.
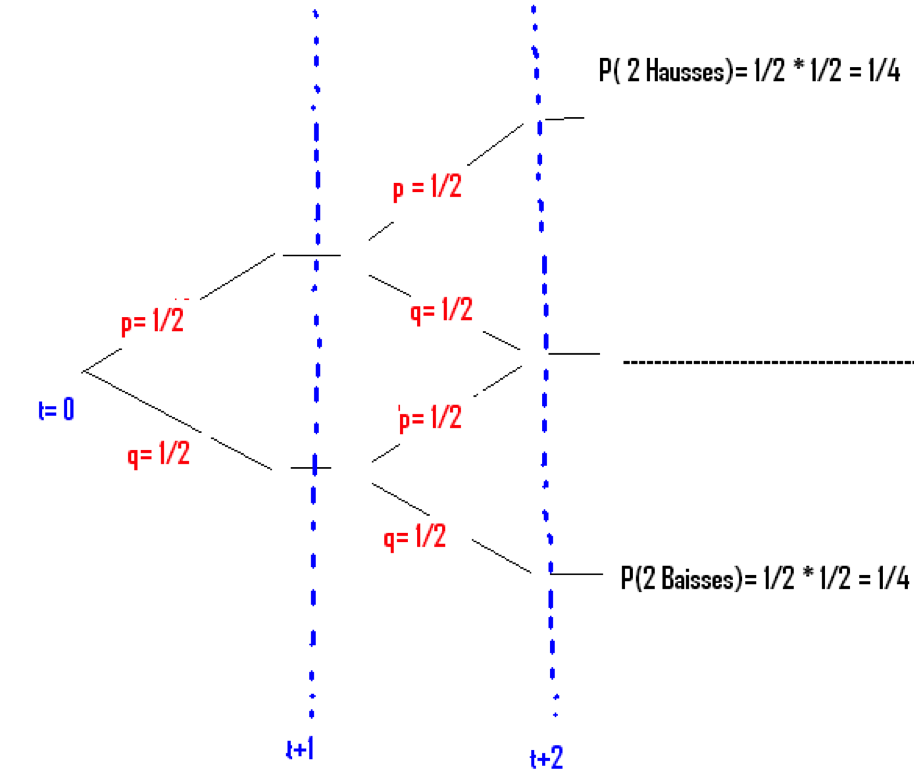
Dans notre modèle de Scalping Contrarien, on attendra qu’il intervienne le mouvement pour jouer son contre-mouvement.
En fonction de l’agressivité du Scalpeur, on pourra n’attendre que les simples mouvements ou bien les doubles, où ces mouvements sont moins nombreux, mais nos points d’entrées sont plus nombreux.
Vu que le Scalping est basé sur le principe de la multiplication des trades, il y aura un arbitrage à faire en terme de E ( X ) entre :
- un Trading agressif (arbres à 2 temps) où on aura + de trades, donc + de trades perdants, mais aussi + de trades gagnants, et
- un Trading plus sécuritaire (arbres à 3 temps), avec – des trades, donc moins de trades perdants par rapport aux gagnants au vu des probabilités.
Ainsi selon l’arbre binomial à 2 temps :
- Un scalpeur qui vend le marché dans son espace temps attitré après une hausse, joue contre la probabilité qu’il y ait 2 hausses, donc il joue contre la probabilité de 1/4.
=> Sa probabilité de gain est donc de : 1 – ¼ = ¾ = 75 %
- Un scalpeur qui achète le marché dans son espace temps attitré après une baisse, joue contre la probabilité qu’il y ait 2 baisses, donc il joue contre la probabilité de 1/4.
=> Sa probabilité de gain est donc de : 1 – ¼ = ¾ = 75 %
Le scalpeur gagnera don 3 fois sur 4 son gain moyen et 1 fois sur 4, il devra gérer sa perte (qui au maximum sera son Stop Loss) mais au vu de l’explication de la contrainte de gain du Scalpeur (Cf. Article Janvier 2012), il tentera de minimiser cette perte de manière à ce que son E(X) soit > 0 dans ce modèle de Scalping Contrarien agressif.
2. Représentation des probabilités a priori et a postériori sur un arbre binomial à 3 temps.
Ainsi selon l’arbre binomial à 3 temps :
- Un scalpeur qui vend le marché dans son espace temps attitré après 2 hausses, joue contre la probabilité qu’il y ait 3 hausses, donc il joue contre la probabilité de 1/8.
=> Sa probabilité est donc de : 1 – 1/8 =7/8 = 85 %
- Un scalpeur qui achète le marché dans son espace temps attitré après 2 baisses, joue contre la probabilité qu’il y ait 3 baisses, donc il joue contre la probabilité de 1/8.
=> Sa probabilité est donc de : 1 – 1/8 = 7/8 = 85 %
Le scalpeur gagnera don 7 fois sur 8 son gain moyen et 1 fois sur 8, il devra gérer sa perte ( qui au maximum sera son Stop Loss) mais au vu de l’explication de la contrainte de gain du Scalpeur(Cf. Post précédent),il tentera de minimiser cette perte de manière à ce que son E(X) soit > 0 dans ce modèle de Scalping Contrarien sécuritaire.
Les vidéos de Trading de la Diamond Trading Academy
En attendant la suite de cet article, vous pouvez commercer à vous former en ligne avec nos vidéos de cours Trading théoriques et nos vidéos Trading pratiques associées.
Cours Trading théoriques Vidéos Trading Pratiques Formation Trading physique





'La logique du Scalping Contrarien 9/16' have 2 comments
29 août 2014 @ 1:04 Zechatdoc
Si je suis bien votre logique, après 2 tirages a pile ou face sortants pile-pile , vous jouez face pour le 3eme tirage avec une probabilité de gain de 85% ?
Si tel est le cas, je veux bien jouer à pile ou face avec vous… on attend 2 tirages identiques, sur le 3eme tirage vous misez 80 sur le côté de votre choix et moi 20 car même ainsi votre espérance de gain reste positive. Le gagnant empoche les 100.
30 septembre 2014 @ 12:19 Marc Antoine Adam de Villiers
Vous n’avez donc pas compris la logique cher Monsieur.
Les probabilités sont calculées a priori(donc avant que les 2 événements arrivent)et non pas après que les 2 événements soient apparus.
Donc oui je suis ok de parier avec vous à t=0, qu’il n’ y a aura pas 3 fois pile,et cette proba n’est absolument pas la même que après 2 piles, on fait la proba qu’il y ait de nouveau un pile.
Ce sont les fameuses probas conditionnelle et si vous n’êtes pas d’accord avec celles-ci,je ne sais que vous dire,ce n’est pas moi qui ait inventé ce théorème, je ne fais que l’appliquer : http://www.chups.jussieu.fr/polys/biostats/poly/POLY.Chp.4.html